Cправочник математических формул
Примеры и задачи с решениями

Алфавитный указатель а б в г д е ж з и к л м н о п р с т у ф х ц ч ш щ э ю я
• Примеры решения задач
• Некоторые постоянные
• Элементарная геометрия
• Геометрические преобразования
• Начала анализа и алгебры
• Уравнения и неравенства
• Аналитическая геометрия
• Высшая алгебра
• Дифференциальное исчисление
• Дифференциальная геометрия
• Интегральное исчисление
• Комплексный анализ
• Элементы теории поля
• Тензорное исчисление
• Дифференциальные уравнения
• Математическая логика
• Теория вероятностей и
математическая статистика
|
Формулы / Интегральное исчисление / Интегралы от функций нескольких переменных / 1 2 3 4 5 6 7 8 9 10 11
Если D - односвязная область, то Первообразная дифференциального выражения Если в односвязной области D для функций P и Q выполняется условие Эйлера
Кри-2 от выражения, являющегося полным дифференциалом, не
зависит от формы пути, соединяющего точки
|
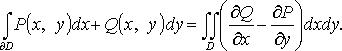
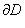 (граница области D) - простая замкнутая кривая,
обход по которой совершается против часовой стрелки. Если D - неодносвязна, то
(граница области D) - простая замкнутая кривая,
обход по которой совершается против часовой стрелки. Если D - неодносвязна, то 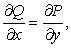 то дифференциальное выражение
то дифференциальное выражение 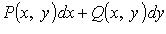 является полным дифференциалом, т. е. существует функци u = u(x, y) (первообразная), такая, что
является полным дифференциалом, т. е. существует функци u = u(x, y) (первообразная), такая, что
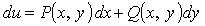 всюду в области D. Первообразная может быть вычислена по одной из формул:
всюду в области D. Первообразная может быть вычислена по одной из формул: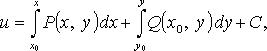
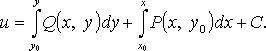
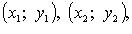 и может быть вычислен
с помощью формулы двойной подстановки:
и может быть вычислен
с помощью формулы двойной подстановки: