Cправочник математических формул
Примеры и задачи с решениями

Алфавитный указатель а б в г д е ж з и к л м н о п р с т у ф х ц ч ш щ э ю я
• Примеры решения задач
• Некоторые постоянные
• Элементарная геометрия
• Геометрические преобразования
• Начала анализа и алгебры
• Уравнения и неравенства
• Аналитическая геометрия
• Высшая алгебра
• Дифференциальное исчисление
• Дифференциальная геометрия
• Интегральное исчисление
• Комплексный анализ
• Элементы теории поля
• Тензорное исчисление
• Дифференциальные уравнения
• Математическая логика
• Теория вероятностей и
математическая статистика
|
Формулы / Тензорное исчисление / Тензоры. Определения и примеры / 1 2 3
Контравариантный вектор - совокупность упорядоченных
систем n чисел, сопоставленных каждому базису данного пространства таким образом, что переход от
системы, сопоставленной одному базису, к системе, сопоставленной другому базису, происходит по закону
С этой точки зрения координаты вектора
Ковариантные векторы Ковариантный вектор - совокупность упорядоченных систем n
чисел, сопоставленных каждому базису данного пространства таким образом, что переход от
системы, сопоставленной одному базису, к системе, сопоставленной другому базису, происходит по закону
Законы преобразования чисел, являющихся произведениями компонент векторов Если
Если
Если
Если
|
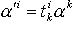 или
или 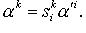
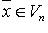 образуют контравариантный вектор. Слово "контравариантный"
означает "измениющийся в обратном направлении" (здесь учтено, что при переходе от одного базиса к другому
векторы и их координаты соответственно преобразуются с помощью обратных матриц).
образуют контравариантный вектор. Слово "контравариантный"
означает "измениющийся в обратном направлении" (здесь учтено, что при переходе от одного базиса к другому
векторы и их координаты соответственно преобразуются с помощью обратных матриц).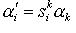 или
или 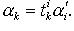 Слово "ковариантный"
означает "изменяющийся так же" (здесь учтено, что законы преобразования рассматриваемых систем чисел
совпадают с законами преобразования базисных векторов). Примером ковариантного вектора служат коэффициенты
линейной формы: если
Слово "ковариантный"
означает "изменяющийся так же" (здесь учтено, что законы преобразования рассматриваемых систем чисел
совпадают с законами преобразования базисных векторов). Примером ковариантного вектора служат коэффициенты
линейной формы: если 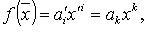 то
то 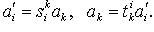
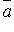 и
и 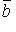 - контравариантные векторы, то:
- контравариантные векторы, то: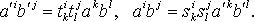
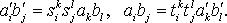
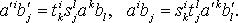
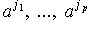 - компоненты
p контравариантныx векторов,
- компоненты
p контравариантныx векторов, 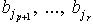 - компоненты q ковариантных
векторов (p + q = r), то совокупность nr чисел, являющихся произведениями компонент этих
векторов, при переходе от одного базиса к другому преобразуется по закону
- компоненты q ковариантных
векторов (p + q = r), то совокупность nr чисел, являющихся произведениями компонент этих
векторов, при переходе от одного базиса к другому преобразуется по закону