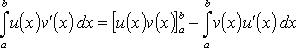Cправочник математических формул
Примеры и задачи с решениями
Алфавитный указатель а б в г д е ж з и к л м н о п р с т у ф х ц ч ш щ э ю я
• Примеры решения задач
• Некоторые постоянные
• Элементарная геометрия
• Геометрические преобразования
• Начала анализа и алгебры
• Уравнения и неравенства
• Аналитическая геометрия
• Высшая алгебра
• Дифференциальное исчисление
• Дифференциальная геометрия
• Интегральное исчисление
• Комплексный анализ
• Элементы теории поля
• Тензорное исчисление
• Дифференциальные уравнения
• Математическая логика
• Теория вероятностей и
математическая статистика
Формулы / Интегральное исчисление / Определенный интеграл / 1 2 3 4 5 6 7 8
Преобразование интеграловИнтегрирование по частям
или
(u, v непрерывно дифференцируемы на интервале Замена переменного (интегрирование подстановкой) Если функция x = x(u) непрерывно дифференцируема на интервале
Дифференцирование по параметру Если функция
Первая формула остается в силе и для несобственных интегралов, если предположить, что интеграл |
).
, а функция f(x) непрерывна на интервале 
, где m - точная нижняя, а M - точная верхняя граница функции x(u) на интервале 
и ее частная производная 
непрерывны на множестве 
, а функции 
и 
дифференцируемы на интервале 
и удовлетворяют на нем условиям 
, то при 
(правило Лейбница).
сходится, а интеграл 
равномерно сходится на интервале 
или на множестве 
.)