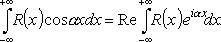Cправочник математических формул
Примеры и задачи с решениями

Алфавитный указатель а б в г д е ж з и к л м н о п р с т у ф х ц ч ш щ э ю я
• Примеры решения задач
• Некоторые постоянные
• Элементарная геометрия
• Геометрические преобразования
• Начала анализа и алгебры
• Уравнения и неравенства
• Аналитическая геометрия
• Высшая алгебра
• Дифференциальное исчисление
• Дифференциальная геометрия
• Интегральное исчисление
• Комплексный анализ
• Элементы теории поля
• Тензорное исчисление
• Дифференциальные уравнения
• Математическая логика
• Теория вероятностей и
математическая статистика
Стоматология в Красноярске https://sapfircs.ru Сапфир
|
Формулы / Комплексный анализ / Комплексные функции / 1 2 3 4 5 6 7 8 9 10
Если f(z) - аналитическая на границе
(обход контура положительный). Вычисление интегралов от функций действительной переменной 1. 2. Если R(x) - рациональная функция, а
где zk - все особые точки функции R(z), лежащие в верхней полуплоскости (Im zk > 0). Если
3. Если R(x) - рациональная функция,
не обращающаяся в нуль на действительной оси,
(zk - все особые точки, лежащие в верхней полуплоскости);
( Замечание.
|
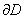 области D
и внутри области, за исключением конечного числа особых точек z1, z2, ...,
zn, лежащих в D, то
области D
и внутри области, за исключением конечного числа особых точек z1, z2, ...,
zn, лежащих в D, то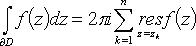
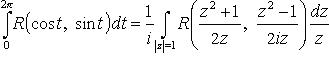 (R - рациональная
функция двух переменных).
(R - рациональная
функция двух переменных).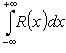 сходится, то
сходится, то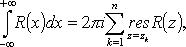
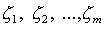 - особые точки
функции R(z), лежащие в нижней полуплоскости, то
- особые точки
функции R(z), лежащие в нижней полуплоскости, то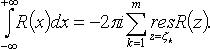
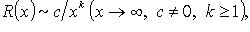 то
то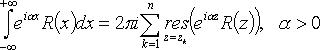
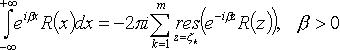
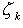 - все особые точки, лежащие в нижней полуплоскости).
- все особые точки, лежащие в нижней полуплоскости).