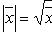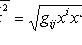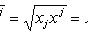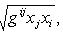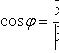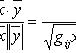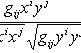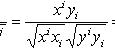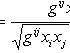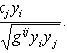Cправочник математических формул
Примеры и задачи с решениями

Алфавитный указатель а б в г д е ж з и к л м н о п р с т у ф х ц ч ш щ э ю я
• Примеры решения задач
• Некоторые постоянные
• Элементарная геометрия
• Геометрические преобразования
• Начала анализа и алгебры
• Уравнения и неравенства
• Аналитическая геометрия
• Высшая алгебра
• Дифференциальное исчисление
• Дифференциальная геометрия
• Интегральное исчисление
• Комплексный анализ
• Элементы теории поля
• Тензорное исчисление
• Дифференциальные уравнения
• Математическая логика
• Теория вероятностей и
математическая статистика
https://relatoseroticos-club.com/zoofilia а
Формулы / Тензорное исчисление / Тензоры в евклидовом пространстве / 1 2
Тензоры в евклидовом пространствеМетрический тензор пространства Из аксиом евклидова пространства следует, что оно может быть определено как такое линейное пространство, в котором задана положительно-определенная квадратичная форма. Другими словами, евклидово пространство - это такое линейное пространство, в котором задан симметрический тензор gij типа Терзор gij называется фундаментальным метрическим тензором пространства. Если Компоненты матрицы gij, обратной матрице gij, образуют дважды контравариантный тензор, называемый контравариантным метрическим тензором. Справедливы формулы xj = gijxi. Поднятие и опускание индекса Переход от контравариантных координат вектора к его ковариантным координатам по формулам xi = gikxk называют опусканием индекса, а переход от ковариантных координат к контравариантным по формулам xj = gijxi - поднятием индекса. Операцию опускания или поднятия индекса в евклидовом пространстве применяют к тензорам любого строения. Например, Длина вектора. Угол между векторами
-1-2- |
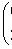
 , такой, что gijxixj > 0 для всех ненулевых векторов.
, такой, что gijxixj > 0 для всех ненулевых векторов.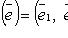
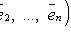 - базис пространства En, то
- базис пространства En, то 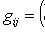
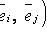 . Числа xi = gikxk (свертка метрического тензора с вектором
. Числа xi = gikxk (свертка метрического тензора с вектором 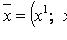
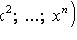 ) называются ковариантными координатами вектора
) называются ковариантными координатами вектора 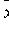
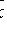 в отличие от его контравариантных координат xi. Ковариантные координаты - это проекции вектора
в отличие от его контравариантных координат xi. Ковариантные координаты - это проекции вектора 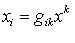
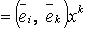
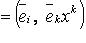
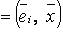 . В ортонормированном базисе xi = xi.
. В ортонормированном базисе xi = xi.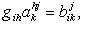
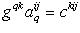 .
.