Cправочник математических формул
Примеры и задачи с решениями

Алфавитный указатель а б в г д е ж з и к л м н о п р с т у ф х ц ч ш щ э ю я
• Примеры решения задач
• Некоторые постоянные
• Элементарная геометрия
• Геометрические преобразования
• Начала анализа и алгебры
• Уравнения и неравенства
• Аналитическая геометрия
• Высшая алгебра
• Дифференциальное исчисление
• Дифференциальная геометрия
• Интегральное исчисление
• Комплексный анализ
• Элементы теории поля
• Тензорное исчисление
• Дифференциальные уравнения
• Математическая логика
• Теория вероятностей и
математическая статистика
Формулы / Бесконечно малые величины
Бесконечно малые величины1. Если переменная величина xn имеет своим пределом нуль lim xn = 0, то она называется бесконечно малой. Это же определение можно высказать и в другой формулировке: Переменная величина xn назвается бесконечно малой, если для всякого наперед заданного положительного числа Ни одно число, кроме нуля, не может быть отнесено к бесконечно малым величинам. 2. Алгебраическая сумма нескольких бесконечно малых величин есть также величина бесконечно малая. Алгебраической суммой называется такая сумма, члены которой присоединяются друг к другу не только при помощи знака плюс, но и при помощи знака минус. 3. Разность двух бесконечно малых величин есть величина бесконечно малая. 4. Произведение ограниченной переменной величины на бесконечно малую есть величина бесконечно малая. Отсюда следует: а) Произведение постоянной величины на бесконечно малую есть величина бесконечно малая. б) Произведение переменной величины, стремящейся к пределу, на бесконечно малую есть величина бесконечно малая. в) Произведение двух бесконечно малых величин есть величина бесконечно малая. 5. Отношение двух бесконечно малых величин не обязательно есть величина бесконечно малая. Отношение двух бесконечно малых величин может быть величиной конечной, бесконечно малой и даже бесконечно большой величиной. Об отношении двух бесконечно малых величин иногда говорят, что оно представляет собой "неопределенность" вида Вычисление предела отношения двух бесконечно малых часто называется также раскрытием "неопределенности" вида |
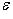 можно указать такое натуральное число N, что | xn | <
можно указать такое натуральное число N, что | xn | < 