Cправочник математических формул
Примеры и задачи с решениями
Алфавитный указатель а б в г д е ж з и к л м н о п р с т у ф х ц ч ш щ э ю я
• Примеры решения задач
• Некоторые постоянные
• Элементарная геометрия
• Геометрические преобразования
• Начала анализа и алгебры
• Уравнения и неравенства
• Аналитическая геометрия
• Высшая алгебра
• Дифференциальное исчисление
• Дифференциальная геометрия
• Интегральное исчисление
• Комплексный анализ
• Элементы теории поля
• Тензорное исчисление
• Дифференциальные уравнения
• Математическая логика
• Теория вероятностей и
математическая статистика
Формулы / Теория вероятностей и математическая статистика / Математическая статистика / 1 2 3
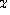  распределения случайной величины X
В дискретном случае
где В абсолютно непрерывном случае
где Доверительные интервалы с коэффициентом доверия p в случае нормально распределенной генеральной совокупности 1. Для математического ожидания при известной дисперсии
где tp - корень уравнения 2. Для математического ожидания при неизвестной дисперсии
s2 - выборочная дисперсия; tp удовлетворяет условию P(|tn-1| < tp) = p; tn-1 - случайная величина, распределенная по закону Стьюдента с n - 1 степенями свободы. 3. Для дисперсии
где
|
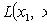
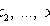
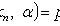
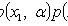
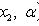
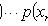
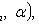
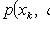
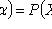
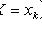
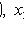
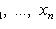- выборочные значения.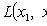
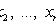
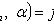
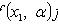
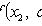
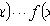
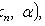
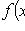
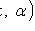- плотность распределения X.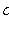
; 
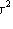
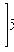
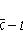
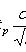
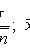
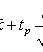
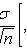
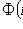
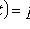
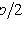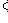
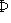- функция Лапласа.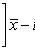
, 
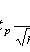
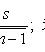
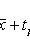
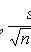
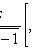
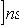
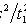
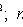
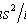
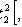
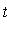
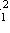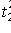
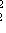находятся из условий: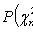
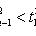
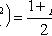
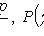
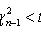
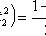
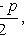
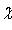
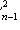- случайная величина, распределенная по закону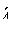 
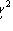с n - 1 степенями свободы.